A workshop on Pandag-related topics will take place on May 15th and 16th at LIP6, on the Pierre and Marie Curie campus.
List of participants:
– Olivier Bodini
– Julien Courtiel
– Oriane Crouzet
– Amaury Curiel
– Matthieu Dien
– Khaydar Nurligareev
– Antoine Genitrini
– Bernhard Gittenberger
– Rémi Maréchal
– Mehdi Naima
– Élie de Panafieu
– Martin Pépin

Schedule of the wokshop:
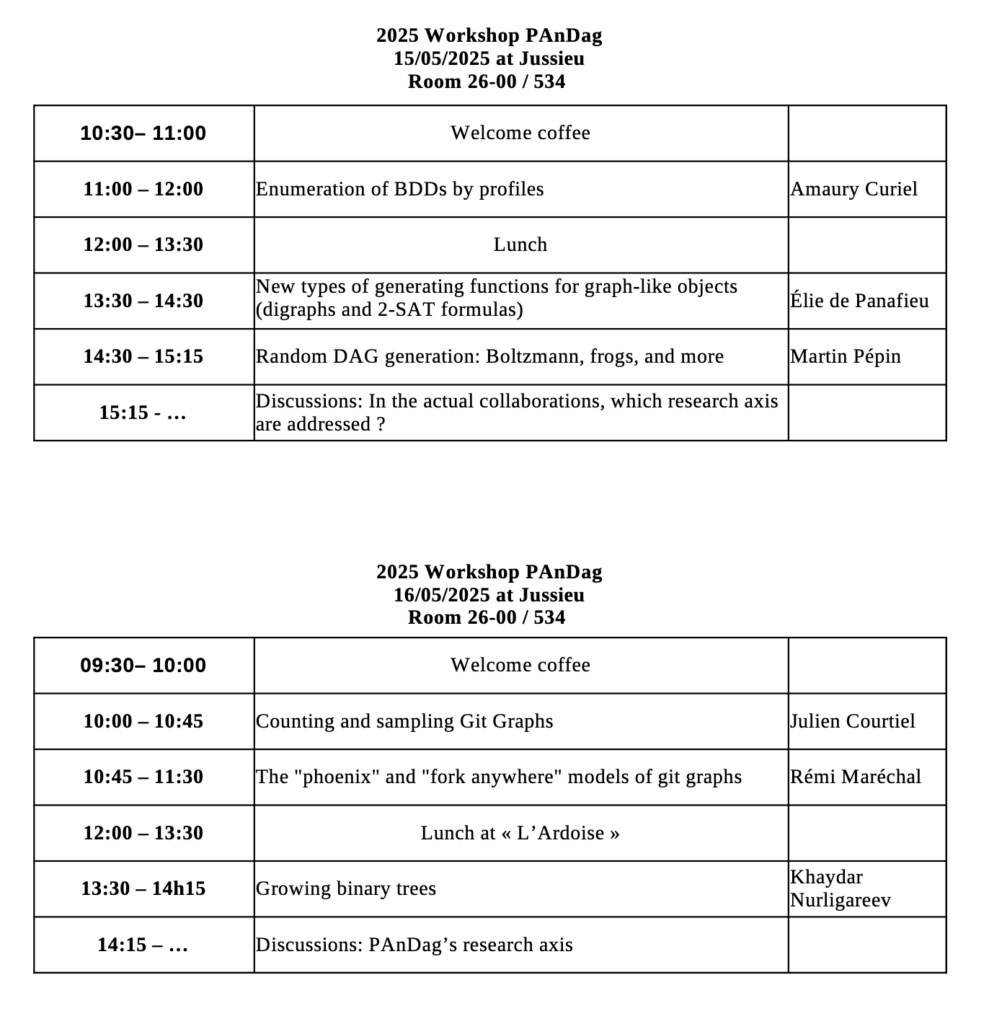
Amaury Curiel : Enumeration of BDDs by profiles
In this presentation, we will examine the different representations of a ubiquitous data structure in computer science: decision trees. This data structure is widely used in machine learning, particularly for solving classification problems via the random forests method. However, this data structure is very memory inefficient due to its exponential size relative to the number of decision variables in the considered problem. This is why in the 1990s, researchers proposed compressing these decision trees by applying various compression techniques, giving rise to a new class of DAGs: BDDs. In this presentation, we will focus on enumerating and generating by profile these different classes of BDDs, extending the results obtained by J. Clément and A. Genitrini in [1] in the context of ROBDDs to other classes of BDDs. We will also examine the enumeration of BDD profiles based on their number of decision variables.
[1] J. Clément and A. Genitrini, “An Iterative Approach for Counting Reduced Ordered Binary Decision Diagrams,” MFCS 2023.
Élie de Panafieu: New types of generating functions for graph-like objects (digraphs and 2-SAT formulas)
Counting digraph families, including DAGs and strongly connected components, involved contributions from many researchers (Liskovets, Wright, Stanley, Robinson, Gessel). The most elegant formulation was derived by Robinson (1977) in the form of generating functions of a new type, specially designed for this task. Dovgal, de Panafieu and Ravelomanana (2023) obtained the exact enumeration of satisfiable 2-SAT formulas by introducing another type of generating functions, inspired by the aforementioned one. This presentation will present those works, with the goal to encourage the design of new types of generating functions for other combinatorial families.
Martin Pépin: Random DAG generation: Boltzmann, frogs, and more
The problem of sampling uniform DAGs with a given number of vertices has been approached from different angles since the early 2000s, achieving near-optimal time complexity in the recent years.
I will present a new technique for generating DAGs, building on the frameworks of graphic generating functions and Boltzmann sampling. This opens the windows for exploring other classes of digraphs, and also allows to achieve optimal time complexity using a trick known as leap frogging.
Julien Courtiel: Counting and samplig Git Graphs
Some Version Control Systems, like Git and Mercurial, arrange the history of a project in the form of a Directed Acyclic Graph (yes a DAG, like in “PAnDAG”). What does a typical graph used in this context look like?
With Martin Pépin, we have studied a model of graphs that is both simple and realistic, which we have called “(Feature Branch) Git Graphs”. I’m going to explain how we count these DAGs, and how we design an efficient Boltzmann sampler.
Rémi Maréchal: The “phoenix” and “fork anywhere” models of git graphs
We want to define classes of DAGs suitable for the modelling of Version Control System repositories (such as git). In an effort to broaden the class of so-called “feature branch graphs” (see Courtiel’s talk), we define “phoenix graphs” and “fork anywhere graphs”. We will explore counting, random generation, and bijective problems regarding these new classes.
[Joint work with Julien Clément, Julien Courtiel, and Martin Pépin]
Khaydar Nurligareev: Growing binary trees
